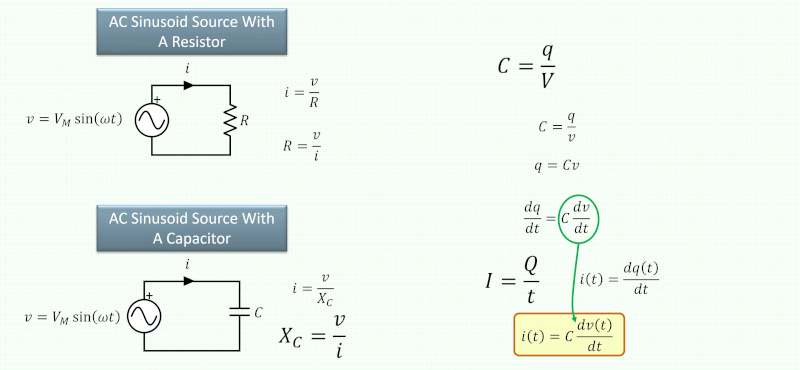
If you’ve dealt with reactance, you surely know the two equations for computing inductive and capacitive reactance. But unless you’ve really dug into it, you may only know the formula the way a school kid knows how to find the area of a circle. You have to have a bit of higher math to figure out why the equation is what it is. [Old Hack EE] wanted to figure out why the formulas are what they are, so he dug in and shared what he learned in a video you can see below.

The key to understanding this is simple. The reactance describes the voltage over the current through the element, just like resistance. The difference is that a resistance is just a single number. A reactance is a curve that gives you a different value at different frequencies. That’s because current and voltage are out of phase through a reactance, so it isn’t as easy as just dividing.

If you know calculus, the video will make a lot of sense. If you don’t know calculus, you might have a few moments of panic, but you can make it. If you think of frequency in Hertz as cycles per second, all the 2π you find in these equations convert Hz to “radian frequency” since one cycle per second is really 360 degrees of the sine wave in one second. There are 2π radians in a circle, so it makes sense.

We love developing intuition about things that seem fundamental but have a lot of depth to them that we usually ignore. If you need a refresher or a jump start on calculus, it isn’t as hard as you probably think. Engineers usually use vectors or imaginary numbers to deal with reactance, and we’ve talked about that too, if you want to learn more.

From Blog – Hackaday via this RSS feed